梯度下降算法的梯度方向

在多元函数中，如果我们沿着函数梯度的方向运动，函数的值会以最快的速度增加；相反，如果我们沿着函数梯度的反方向运动，函数的值会以最快的速度减小。

梯度的基本概念

梯度(gradient)是微积分和向量分析中的重要概念，它可以理解为多元函数全部偏导数所构成的向量。
例如，二元函数f(x,y)的梯度是由函数f对x和y求偏导组成的二维向量。

二元函数与函数上某点的梯度

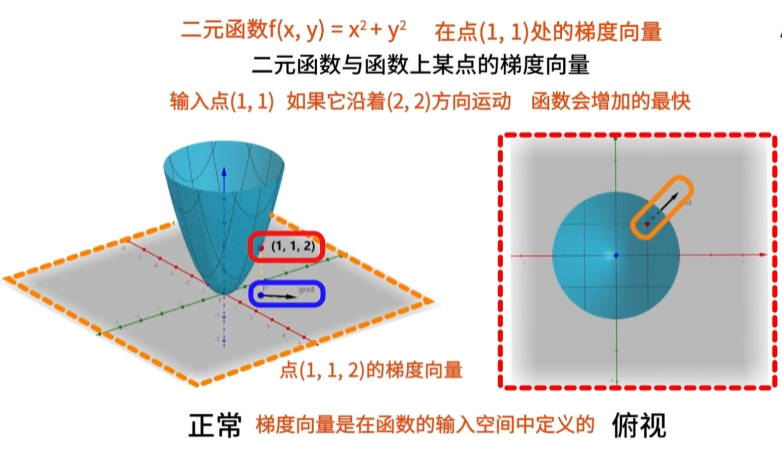
考虑二元函数f(x,y)=x^2+y^2，在点(1,1)处的梯度向量如下图所示。
将函数上的点P(1,1,2)标记为红色，将该点向灰色的x-o-y平面投影，标记为蓝色。
从蓝色点出发，画出向量(2,2)，用黑色箭头表示，这就是点P的梯度向量。

由此可见，从输入点(1,1)沿着(2,2)方向运动，函数会增加最快。

梯度向量的具体算法

从点P出发，向不同方向运动相同长度，可以发现只有沿着梯度方向运动，函数值变化最快。

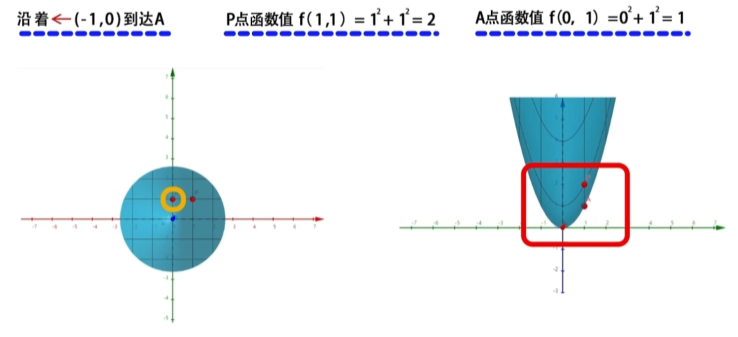
基于俯视角度观察函数，在x-o-y平面上，我们可以沿着三个方向向量：(-1,0), (1,0), (2,2)，移动一个单位。

• 从P点向(-1,0)方向到达A点，A点的函数值为f(0,1) = 0^2 + 1^2 = 1

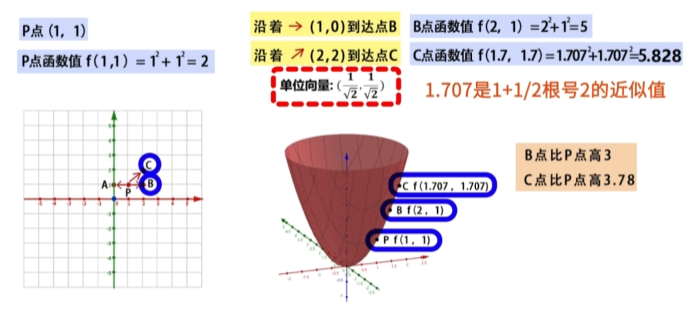
• 从P点向(1,0)方向到达B点，B点的函数值为f(2,1) = 2^2 + 1^2 = 5

• 从P点向(2,2)方向到达C点，C点的函数值为f(1.7,1.7) = 1.7^2 + 1.7^2 = 5.828

在机器学习中，我们通常希望找到目标函数的最小值。
为了达到这个目标，我们可以从某一个点出发，沿着梯度的反方向运动，这样函数的值会以最快的速度减小。
通过这种方式，我们可以更快地将函数收敛到最小值。

总结

梯度下降算法的关键在于选择合适的梯度方向进行更新。

我们通过计算函数的梯度向量，可以确定沿着何种方向函数值变化最快。

在机器学习中，这个概念非常重要，因为我们经常需要通过梯度下降来优化模型的参数。

通过沿着逐渐减小的梯度方向迭代更新参数，我们能够有效地寻找目标函数的最小值。