非线性分类的决策边界

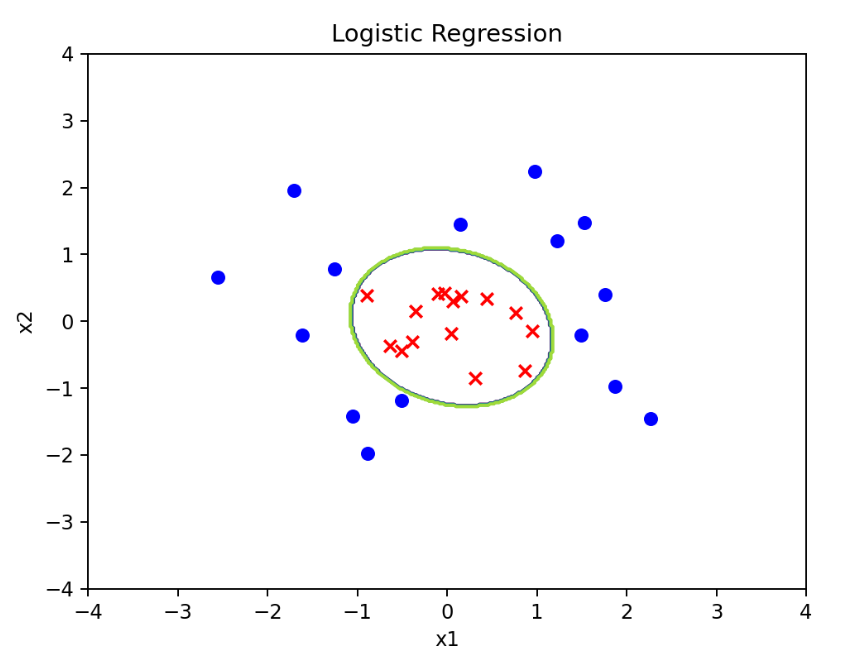
绿色曲线代表了正例和负例的决策边界。
曲线里面是正例，曲线外面是负例，曲线是个椭圆。

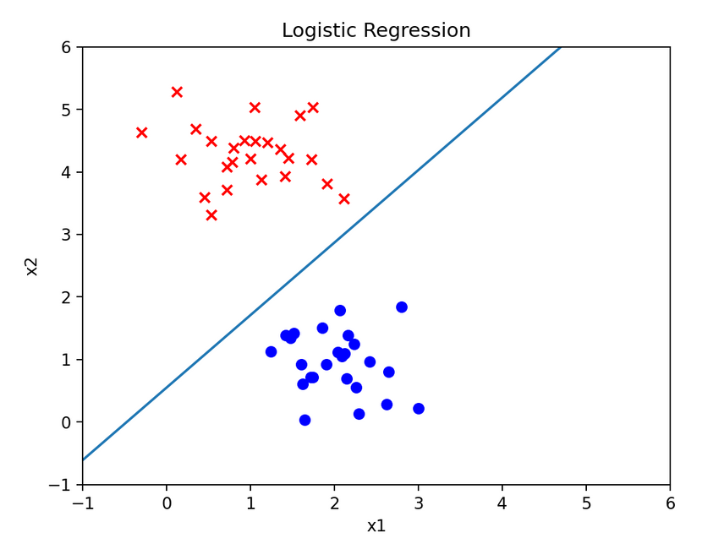
线性分类的决策边界，可以按照直线的绘制方法进行绘制。

分界平面不是线性的，是这种椭圆型状的，又该怎么办呢？

假设使用线性分类的绘制方式。
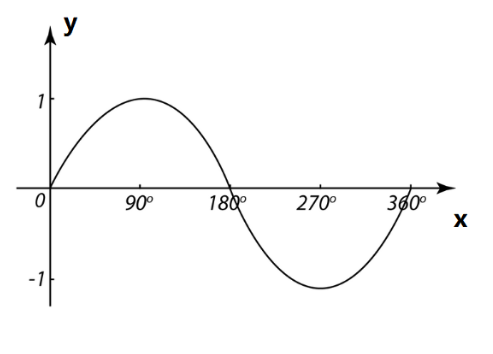
给出x坐标，计算y坐标，再画出曲线。

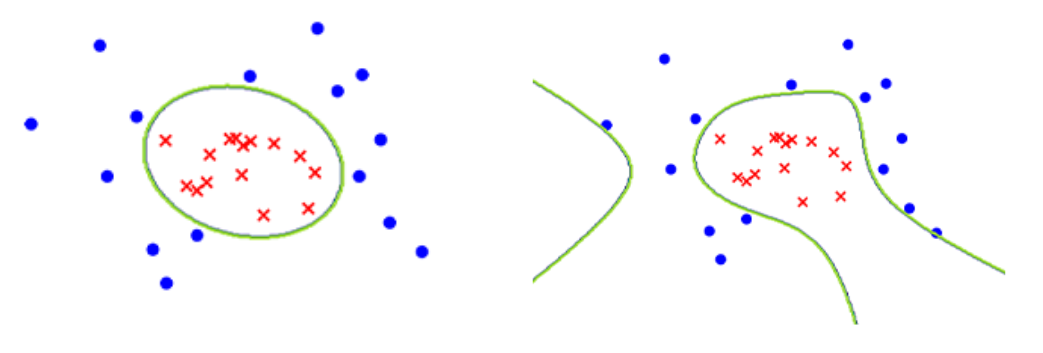
但现在我们想要画的曲线根本就不是函数，它是绿色的不规则曲线。
我们没办法找到一个x对应一个y，所以也就没法用画函数的方法，画出这个绿色的边界。

这种非线性分类的决策边界，需要基于等高线的概念来绘制。

等高线的基本概念

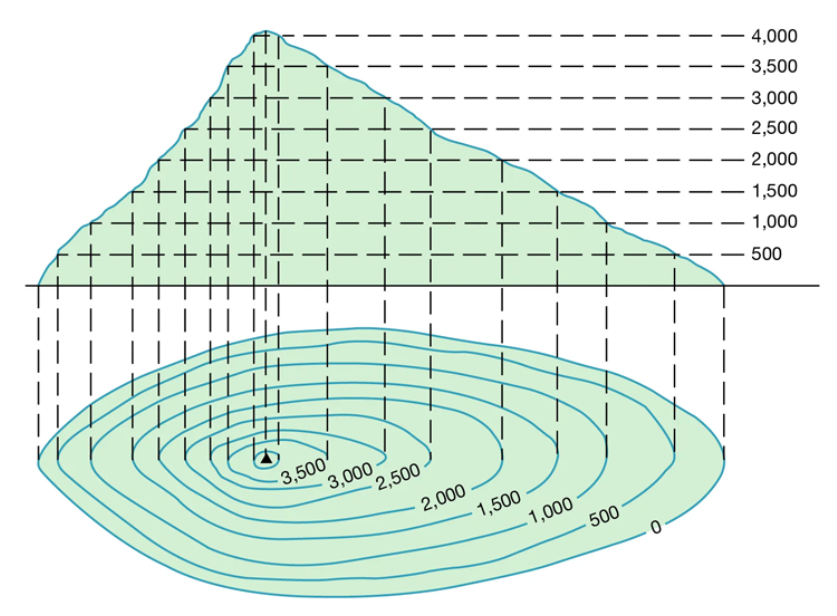
等高线，也被称为等值线，它是一种在二维平面上表示三维地形的方法。

例如，下图使用等高线，描述了某座山的地形图。

其中我们使用黑色三角代表山顶，距离山顶最近的一圈是海拔4000米，然后是3500米，3000米等等到0。
每一圈都对应了一个高度。

将等高线视为类别的边界

我们要将等高线，看做是不同类别的分界面。
不同类别的样本，需要看做是不同的高度，这样，就可以基于不同样本点的高度，绘制出一条等高线了。

例如，这里的蓝色圆圈对应的高度是1，红色叉子对应的高度是0，它们之间就自然产生一条绿色的等高线，对应分类决策边界。

现在假设基于这些样本数据，训练出了非线性分类的模型。
这里忽略掉模型的训练过程，想象此时我们已经有了这个模型。

接着我们要使用这个模型，将平面上所有的样本点，都识别出对应的分类结果，这个结果要么是0，要么是1。

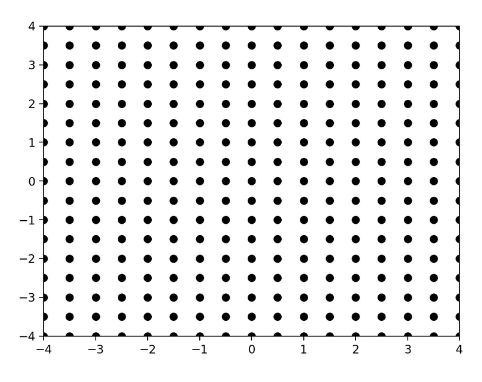
例如，在平面上，如果每隔0.5个单位长度，取一个点，那么从-4到4之间可以取15个点，这样平面上就会产生15乘15一共255个数据点。

将这些数据点作为测试数据，带入到已经训练出的非线性分类的模型。
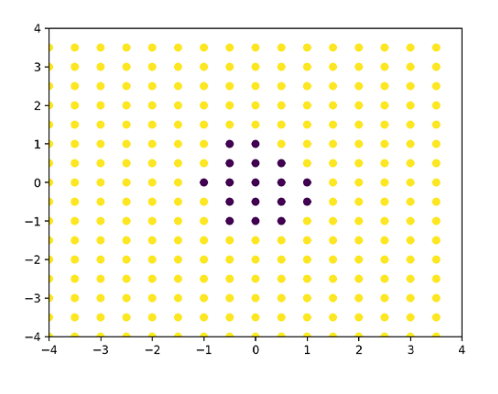
让模型决策这些数据应该是类别0还是类别1，这里类别0是黄色的，类别1是紫色的。
而数据的类别，刚好也对应数据在平面上的高度，即高度0还是高度1。

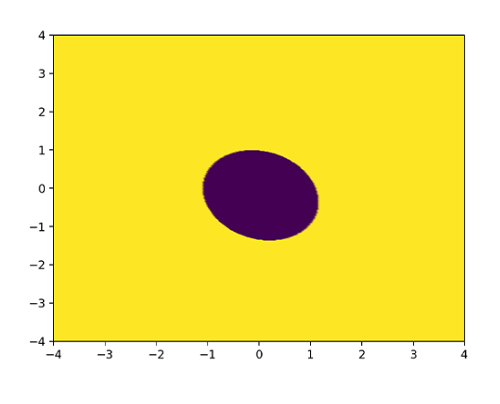
这时，如果我们将测试数据设置足够稠密。
例如，每间隔0.01，取一个点，再将这些点画在平面上，自然就形成一个椭圆形的决策边界了。