Pytorch实现非线性分类
Pytorch实现非线性分类
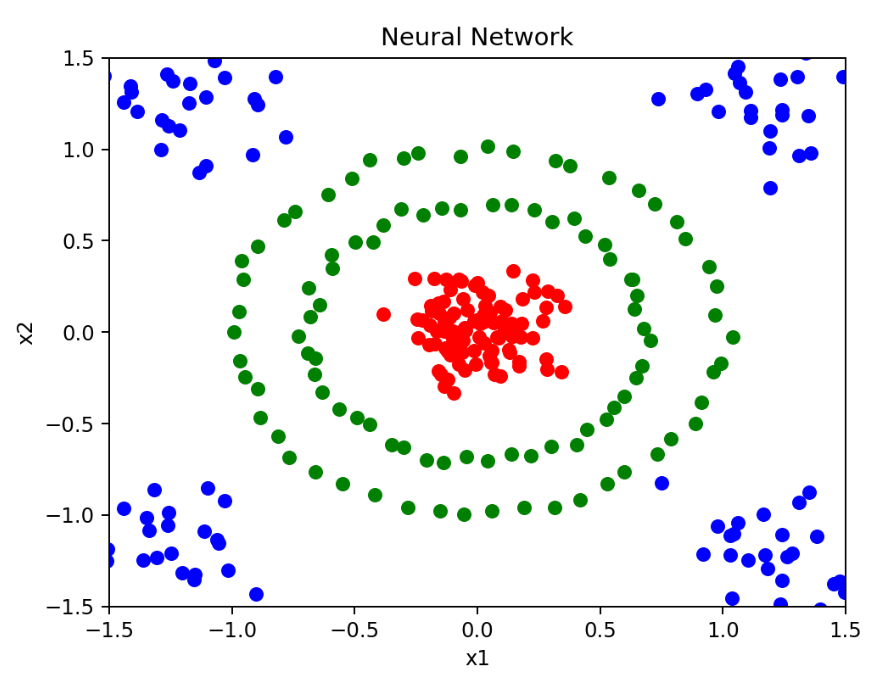
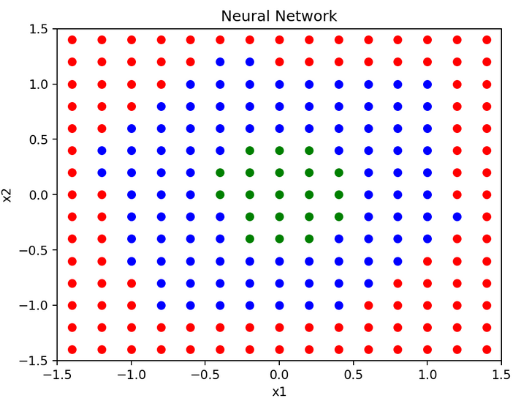
在平面上,包括了3组不同类别的训练数据,分别使用红色、蓝色和绿色表示。
它们呈非线性的分布方式。
基于Pytorch深度学习框架,训练一个神经网络模型,将这三组数据分开。
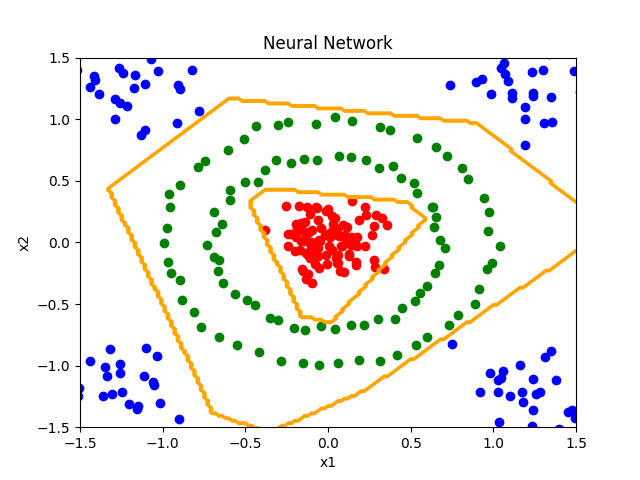
并且,我们要将模型产生的分类决策边界,使用橙色进行标记。
安装并导入Pytorch相关的库
需要安装 scikit-learn、matplotlib、numpy、torch 库。1
2
3
4pip install scikit-learn
pip install matplotlib
pip install numpy
pip install torch torchvision torchaudio
在代码中导入上述安装好的库1
2
3
4
5from sklearn.datasets import make_blobs,make_circles
import matplotlib.pyplot as plt
import numpy as np
import torch.nn as nn
import torch
分类数据的生成
定义函数make_data
函数传入num,代表每种类别的数据个数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21def make_data(num):
# 设定随机数生成器的种子
# 使随机数序列,每次运行时都是确定的
np.random.seed(0)
# 红色数据使用make_blobs生成
# 以(0, 0)为中心的正太分布数据
red, _ = make_blobs(
n_samples=num,centers=[[0, 0]],cluster_std=0.15
)
# 绿色数据用make_circles生成,分布在红色数据的周围
green, _ = make_circles(
n_samples=num,noise=0.02,factor=0.7
)
# 蓝色数据分布在四个角落
blue, _ = make_blobs(
n_samples=num,
centers=[[-1.2, -1.2],[-1.2, 1.2],[1.2, -1.2],[1.2, 1.2]],
cluster_std=0.2
)
# 函数返回三种数据
return red, green, blue定义函数draw_data
函数传入make_data生成的绿色、蓝色和红色三种数据。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15def draw_data(red, green, blue):
# 创建-4到4的平面画板
board = plt.figure()
axis = board.add_subplot(1,1,1)
axis.set(
xlim=[-1.5, 1.5],
ylim=[-1.5, 1.5],
title='Neural Network',
xlabel='x1',
ylabel='x2'
)
# 使用plt.scatter绘制出绿色、蓝色和红色三种数据
plt.scatter(green[:, 0], green[:, 1], color='green')
plt.scatter(blue[:, 0], blue[:, 1], color='blue')
plt.scatter(red[:, 0], red[:, 1], color='red')
神经网络模型的定义
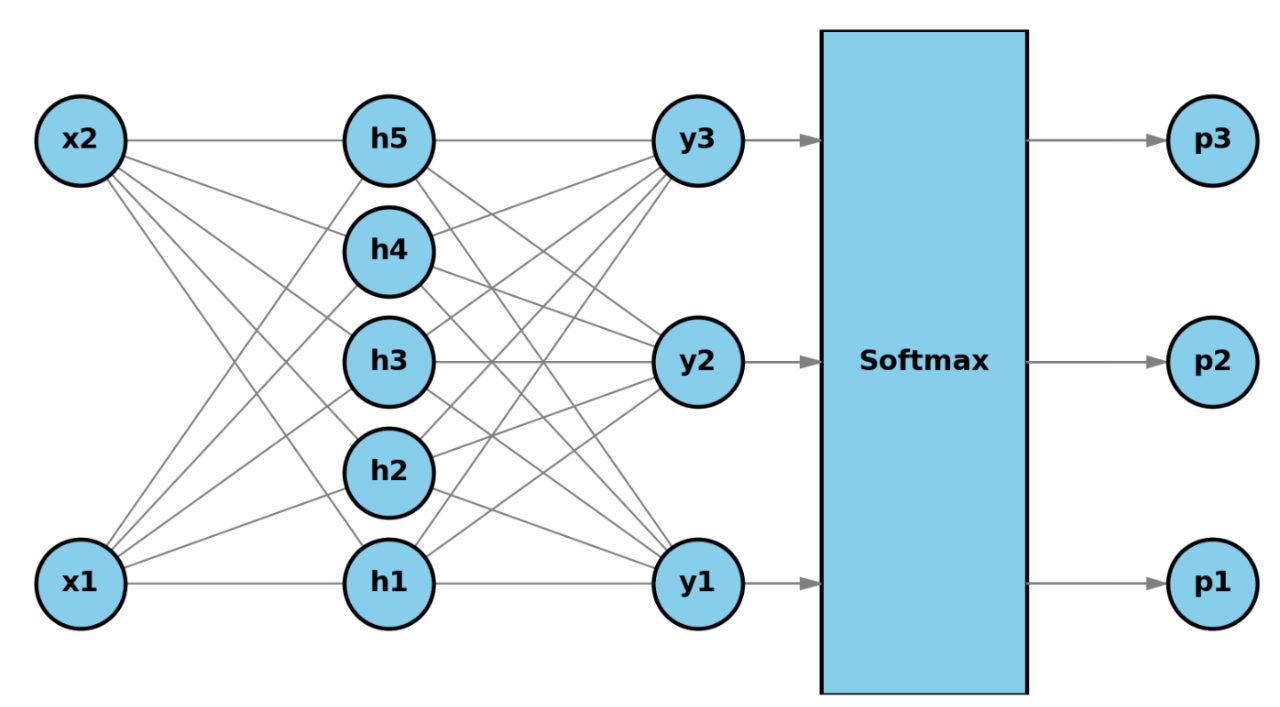
为了解决该分类问题,我们要定义一个三层神经网络。
输入层包括x1和x2两个特征,它们表示平面上,数据点的横坐标和纵坐标。
隐藏层有5个神经元,它们是解决该分类问题的高级特征。
输出层有3个神经元,对应3种不同的类别。
输出层输出的y1、y2、y3,会输入至softmax函数,转换为三种类别的概率,p1、p2和p3。
- 定义神经网络类Network
函数传入参数n_in, n_hidden, n_out,代表输入层、隐藏层和输出层中的神经元数量。1
2
3
4
5
6
7
8
9
10
11
12
13
14# 定义神经网络类Network,它继承nn.Module类
class Network(nn.Module):
def __init__(self, n_in, n_hidden, n_out):
super(Network, self).__init__()
# layer1是输入层与隐藏层之间的线性层
self.layer1 = nn.Linear(n_in, n_hidden)
# layer2是隐藏层与输出层之间的线性层。
self.layer2 = nn.Linear(n_hidden, n_out)
# 实现神经网络的前向传播
def forward(self, x):
x = self.layer1(x) # 计算layer1的结果
x = torch.relu(x) # 进行relu激活
# 计算layer2的结果,并返回
return self.layer2(x)
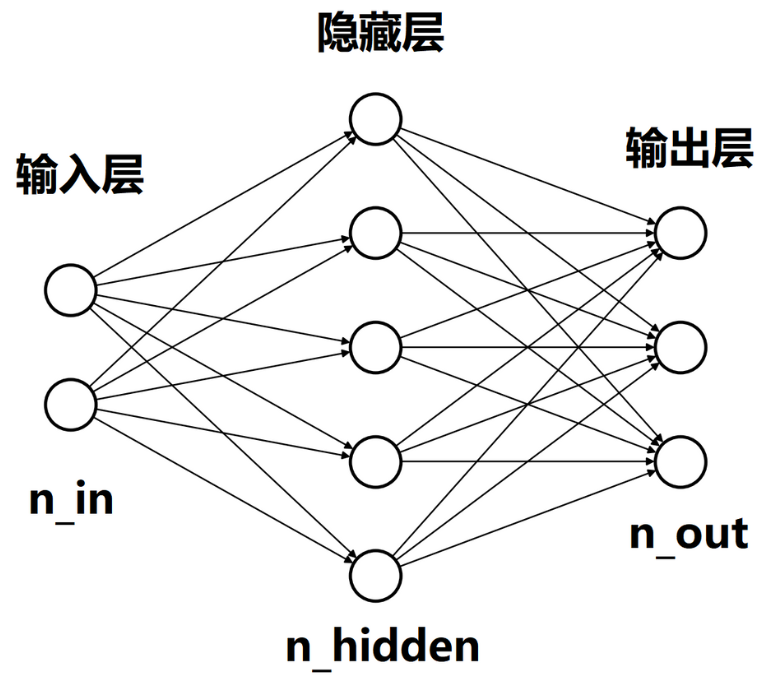
n_in, n_hidden, n_out:输入层、隐藏层和输出层的关系
神经网络模型的训练
完成模型的定义后,训练神经网络模型。
- 定义函数train_network
函数传入make_data生成的绿色、蓝色和红色三种数据。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49def train_network(red, green, blue):
n_features = 2 # 特征数
n_hidden = 5 # 隐藏层神经元个数
n_classes = 3 # 类别数
n_epochs = 10000 # 迭代次数
learning_rate = 0.001 # 学习速率
# 将绿色、蓝色、红色三种样本,从numpy数组转换为张量形式
green = torch.FloatTensor(green)
blue = torch.FloatTensor(blue)
red = torch.FloatTensor(red)
# 一起组成训练数据data
data = torch.cat((red, green, blue), dim=0)
# 设置label保存三种样本的标签
label = torch.LongTensor(
[0] * len(green) + [1] * len(blue) + [2] * len(red)
)
# 创建神经网络模型实例model
model = Network(n_features, n_hidden, n_classes)
# 创建交叉熵损失函数
criterion = nn.CrossEntropyLoss()
# 创建Adam优化器optimizer
optimizer = torch.optim.Adam(
model.parameters(), lr=learning_rate
)
# 进入softmax回归模型的循环迭代
for epoch in range(n_epochs):
# 使用当前的模型,预测训练数据data,结果保存在output中
# 这里即为前向传播
output = model(data)
# 计算预测值output与真实值label之间的损失loss
loss = criterion(output, label)
# 通过自动微分计算损失函数关于模型参数的梯度
loss.backward()
# 更新模型参数,使得损失函数减小
optimizer.step()
# 将梯度清零,以便于下一次迭代
# 这实际上就是反向传播
optimizer.zero_grad()
# 模型的每一轮迭代,有前向传播和反向传播共同组成
if epoch % 1000 == 0:
# 每1000次迭代,打印一次当前的损失
# loss.item对应损失的标量值
print(f'{epoch} iterations: loss = {loss.item()}')
# 返回训练后的模型
return model
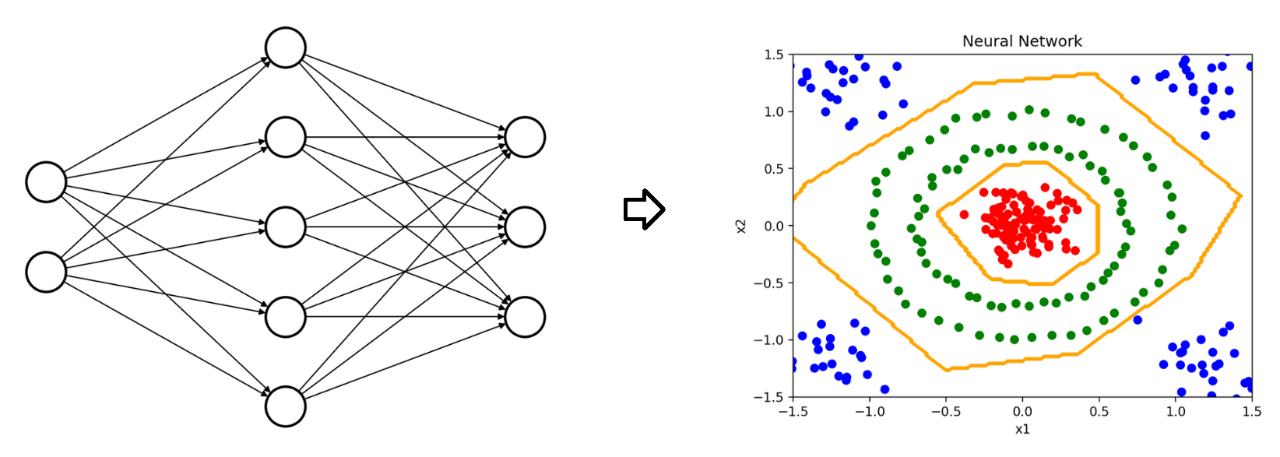
绘制决策边界
生成用于绘制决策边界的等高线数据。
根据已经训练的model,计算对应类别结果。
不同类别的结果会对应不同的高度。
基于数据点的坐标与高度数据,绘制等高线。
- 定义函数draw_decision_boundary
函数传入min-x1到max-x1是画板的横轴范围,min-x2到max-x2是画板的纵轴范围,model是训练好的模型。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25def draw_decision_boundary(minx1, maxx1, minx2, maxx2, model):
# 调用mesh-grid生成网格数据点
# 每个点的距离是0.02,这样生成的点,可以覆盖平面的全部范围。
xx1, xx2 = np.meshgrid(
np.arange(minx1, maxx1, 0.02),
np.arange(minx2, maxx2, 0.02),
)
# 设置x1s、x2s和z分别表示数据点的横坐标、纵坐标和类别的预测结果
x1s = xx1.ravel()
x2s = xx2.ravel()
z = []
# 遍历全部样本
for x1, x2 in zip(x1s, x2s):
# 将样本转为张量
test_point = torch.FloatTensor([[x1, x2]])
# 使用model预测结果
output = model(test_point)
# 选择概率最大的类别
_, predicted = torch.max(output, 1)
# 添加到高度z中
z.append(predicted.item())
# 将z重新设置为和xx1相同的形式
z = np.array(z).reshape(xx1.shape)
# 返回xx1、xx2和z
return xx1, xx2, z
生成每个点的距离是0.02的网格数据点
使用model预测结果,选择概率最大的类别,添加到高度z中。
将平面上的黑色点,标记为红色、绿色、蓝色三种颜色。
main函数绘制决策边界
调用make_data,draw_data,train_network,draw_decision_boundary四个函数。
最后调用plt.contour绘制多分类的决策边界。运行程序,在结果中可以看到橙色的决策边界。
1 | if __name__ == '__main__': |
完整代码示例
1 | from sklearn.datasets import make_blobs,make_circles |