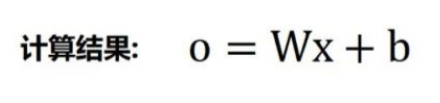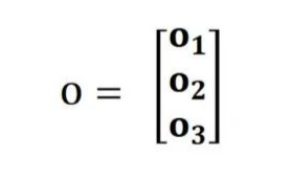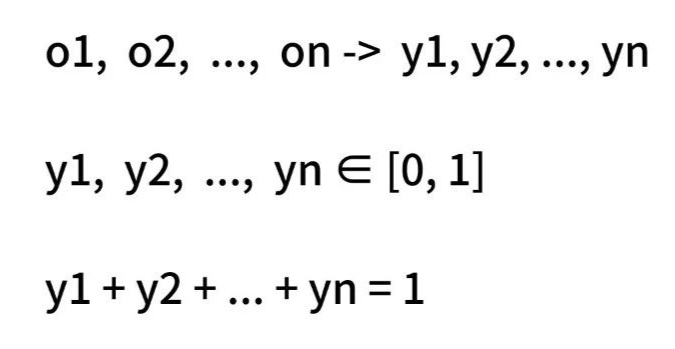softmax回归

在解决多分类问题时，我们可以直接构建一个softmax回归模型，同时对所有类别进行识别。

在softmax回归中，包括了两个步骤。

• softmax线性预测:
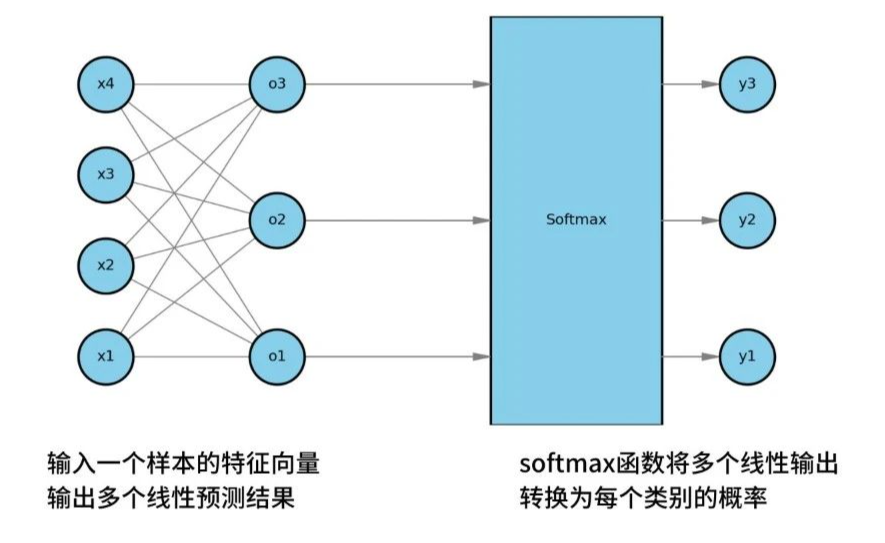
  输入一个样本的特征向量，输出多个线性预测结果。
• softmax计算类别概率:
  将上述结果输入到softmax函数，softmax函数会将多个线性输出，转换为每个类别的概率。

softmax线性预测

在某多分类问题中，有三个目标类别o1、o2、o3，四个输入特征，x1到x4。

softmax回归会基于输入x，计算o1、o2、o3三个线性输出。

在计算每一个线性输出o时，都会依赖一组w和b参数。
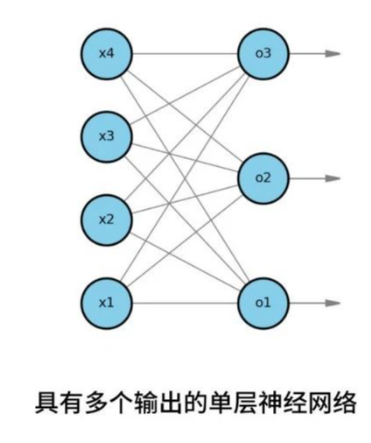
我们可以将softmax回归，看做是一个具有多个输出的单层神经网络。

我们可以基于矩阵，计算线性输出o。

例如，在计算o=Wx+b时。
W是一个34的权重矩阵。
b代表了一个31的偏置列向量。
x是4*1的特征向量。

经过计算，会得到3*1的输出结果o。

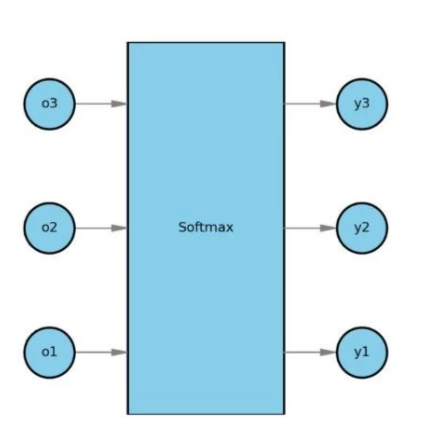
softmax计算类别概率

计算出线性输出o后，将o输入到softmax函数，从而将线性输出o转换为每个类别的预测概率y。

设有n个输出，o1到on。
第k个输出是ok，它对应的类别概率是yk。

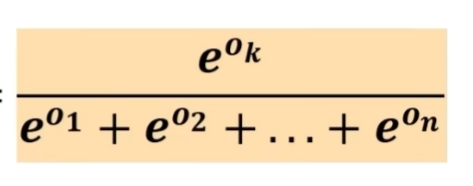
其中yk等于，常数e的ok次方，除以e的o1次方加上e的o2次方，等等到e的on次方，所有指数函数的和。

这样，我们就通过softmax函数，将所有线性输出，都转换为0到1之间的实数了。
并且输出的总和，y1+y2加到yn，这个结果恰好为1。

softmax计算类别概率示例

设输出o1、o2、o3分别等于3个浮点数，0.3、2.9和4.0。
然后计算e的0.3、2.9、4.0次方。

将它们累加到一起，结果是74.12。
然后使用e的oi次方除以74.12，就得到了对应的yi。
这时计算y1+y2+y3的和，结果恰好等于1。

因为y3的值最大，所以最终识别的结果为类别3。

softmax回归的总结

总结来说，softmax函数不会改变线性输出o之间的大小顺序，只会为每个类别分配相应的概率。

softmax回归模型的优势

softmax回归模型的优势在于模型简洁和高效。
我们只需要一次训练，就可以得到同时识别所有类别的多分类模型。

另外，softmax回归也可以很好地处理类别间的互斥问题。
softmax函数可以确保预测结果的总和为1，这在某些使用类别互斥的场景下，非常有用。

softmax回归模型的劣势

不过使用softmax回归也存在着一些问题。

在需要优化模型中的某个类别，或增加新的类别时，会影响到其他所有类别，这样就会产生较高的评估与维护成本。