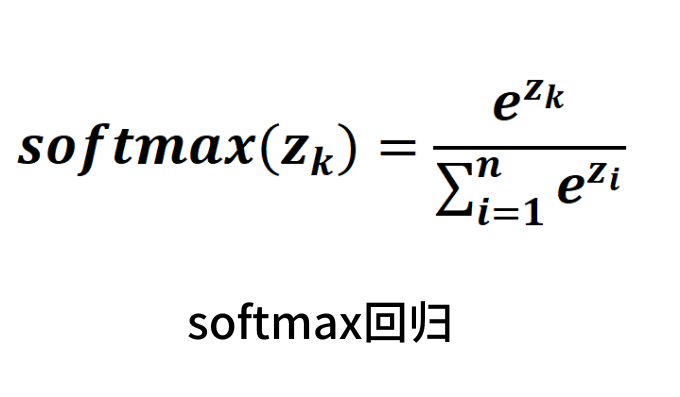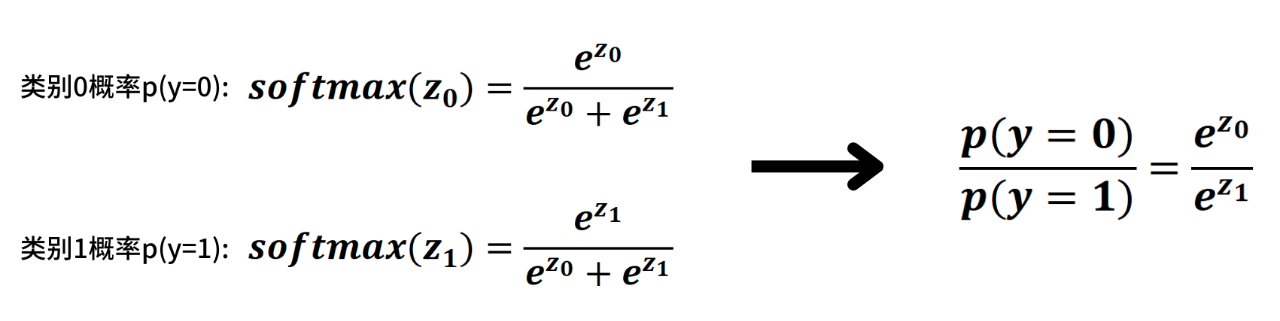softmax与sigmoid
softmax与sigmoid
sigmoid函数是一种常用的非线性函数,也被称为逻辑函数(Logistic function)。
它将任意实数映射到一个介于0和1之间的值。
将线性输出z转化为一个概率,这个概率表示样本属于正例的可能性。
在softmax归中,我们使用softmax函数将输出值zk同样转化为概率,这个概率表示样本属于第k个类别的可能性。
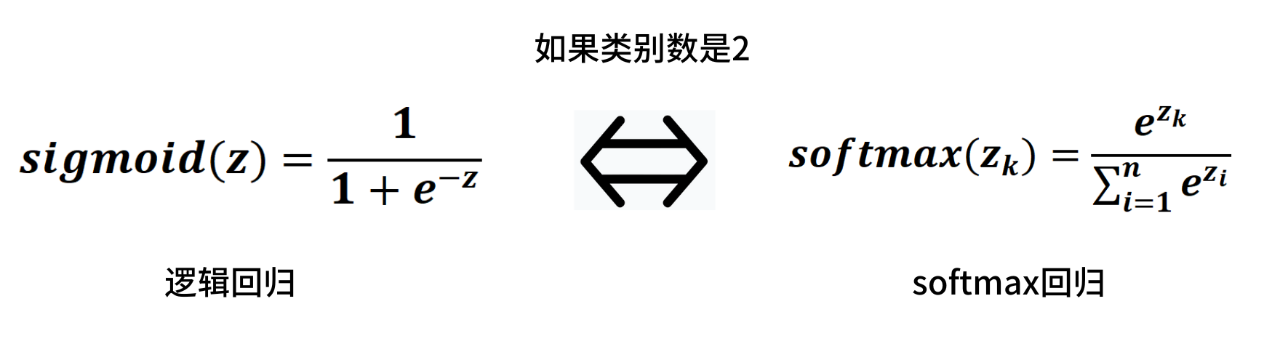
当softmax类别数为2时,softmax回归和逻辑回归的输出等价的。
softmax类别数为2公式推导
设有两个类别,类别1和类别0,某样本x属于1或0的概率为p(y=1)和p(y=0)。
在逻辑回归中,使用sigmoid函数来预测正例的概率,结果p(y=1)=sigmoid(z)。
在softmax回归中,类别k的概率为,softmax(zk)。
根据softmax函数,类别0和类别1的概率分别是softmax(z0)、softmax(z1)。
将这两个等式相除,得到p(y=0)/p(y=1)=e^z0/e^z1。
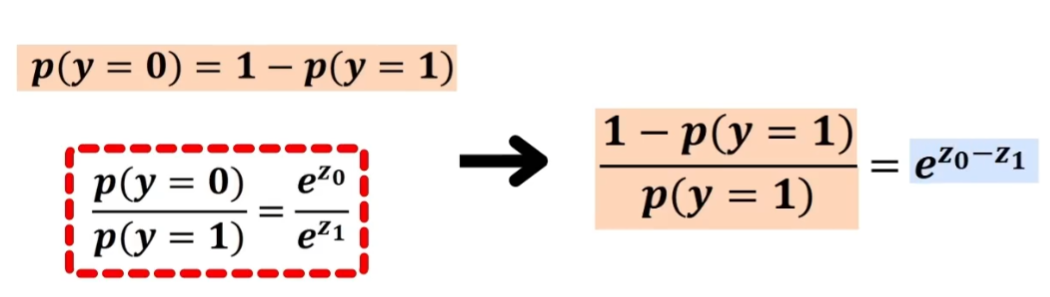
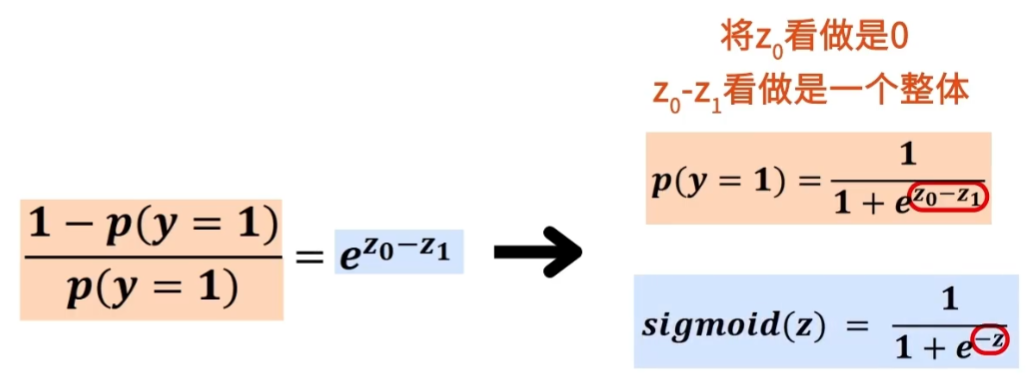
将p(y=0)=1-p(y=1),带入这个式子,得到,(1 - p(y=1)) / p(y=1)= e^(z0-z1)。
将p(y=1),表示出来,得到 1/ (1+e^(z0-z1))。
这时我们将z0看做是0,或者将z0-z1看做是一个整体,对应-z,就会得到逻辑回归的形式了。
可以得出结论,在处理二分类问题时,softmax回归和逻辑回归,实际上是完全等价的模型。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Nero Blog!
评论